概率论中的联合概率是指两个事件同时发生的概率。换句话说,联合概率是两个事件一起发生的可能性。

联合概率公式
![]()
在哪里:
- P(A ⋂ B)是事件“A”和“B”的联合概率的表示法。
- P(A)是事件“A”发生的概率。
- P(B)是事件“B”发生的概率。
联合概率和独立性
要使联合概率计算起作用,事件必须是独立的。换句话说,事件不能相互影响。要确定两个事件是独立的还是相关的,重要的是要问一个事件的结果是否会影响另一个事件的结果。如果一个事件的结果不影响另一事件的结果,则这些事件是独立的。
相关事件的一个例子是天空中有云的概率和那天下雨的概率。天上有云的概率对当天下雨的概率有影响。因此,它们是相关事件。
独立事件的一个例子是两次抛硬币正面朝上的概率。第一次抛硬币正面朝上的概率对第二次抛硬币正面朝上的概率没有影响。
视觉表现
联合概率可以通过维恩图直观地表示。考虑在公平的六面骰子中掷出两个 6 的联合概率:
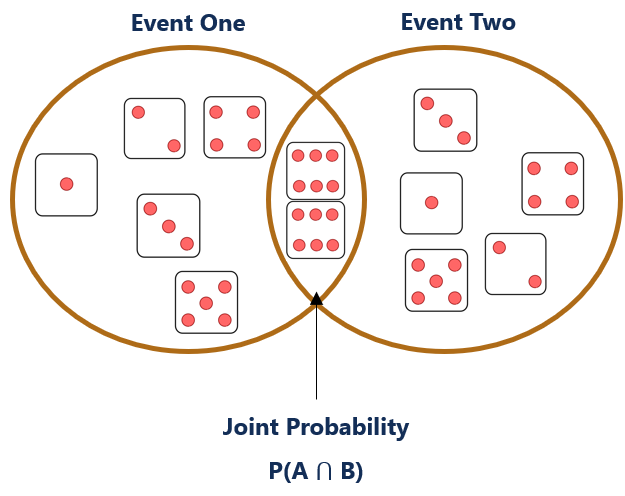
如上面的维恩图所示,联合概率是两个圆圈相互重叠的地方。它被称为“两个事件的交集”。
例子
以下是联合概率的示例:
示例 1
在公平的六面骰子中掷两次数字 5 的联合概率是多少?
事件“A” = 第一次掷出 5 的概率是 1/6 = 0.1666。
事件“B” = 在第二轮掷出 5 的概率是 1/6 = 0.1666。
因此,事件“A”和“B”的联合概率为 P(1/6) x P(1/6) = 0.02777 = 2.8%。
示例 2
在抛硬币中得到正面和反面的联合概率是多少?
事件“A” = 第一次抛硬币正面的概率是 1/2 = 0.5。
事件“B” = 在第二次抛硬币中出现尾巴的概率是 1/2 = 0.5。
因此,事件“A”和“B”的联合概率为 P(1/2) x P(1/2) = 0.25 = 25%。
示例 3
抽到一张黑色的十号牌的联合概率是多少?
事件“A” = 绘制一个的概率 10 = 4/52 = 0.0769
事件“B” = 抽黑卡的概率 = 26/52 = 0.50
因此,事件“A”和“B”的联合概率为 P(4/52) x P(26/52) = 0.0385 = 3.9%。













